小本本系列:大模型中的文本向量text embeddings

作为人类,我们可以阅读并理解文本(至少可以理解一部分),然而计算机“用数字思考”,因此它们无法自动理解单词和句子的含义。如果我们要让计算机理解自然语言,就需要将这些信息转换成计算机可以处理的格式——数字向量。这篇文章就研究一下科学家是如何一步一步让计算机理解和认识人类的语言的。
人们早在多年前就学会了如何将文本转换为机器可理解的格式(最早的版本之一是ASCII)。这种方法有助于渲染和传输文本,但并不编码单词的意义。当时,标准的搜索技术是关键词搜索,即仅查找包含特定单词或N元语法的所有文档。
然后,在几十年后,嵌入式表示(embeddings)出现了。我们可以计算单词、句子甚至图像的嵌入式表示。嵌入式表示也是数字向量,但它们能够捕捉意义。因此,你可以使用它们进行语义搜索,甚至处理不同语言的文档。
词袋模型 bag of words
将文本转换为向量的最基本方法是词袋模型。让我们以理查德·P·费曼的一句名言为例:“我们很幸运生活在一个我们仍在不断发现的时代”。我们将使用这句话来说明词袋模型的方法。
获得词袋向量的第一步是将文本拆分为单词(标记),然后将单词还原为其基本形式。例如,“running”将转换为“run”。这个过程称为词干提取(stemming,即将文本拆分为单词并进行词干提取)。
如下代码所示,用 NLTK 实现词袋模型:
from nltk.stem import SnowballStemmer
from nltk.tokenize import word_tokenize
import nltk
import os
# Resource punkt_tab not found. Try using the NLTK Downloader
if not os.path.exists("./tokenizers/punkt_tab.zip"):
nltk.download("punkt_tab", download_dir="./")
text = "We are lucky to live in an age in which we are still making discoveries"
# tokenization - splitting text into words
words = word_tokenize(text)
print(words)
# ['We', 'are', 'lucky', 'to', 'live', 'in', 'an', 'age', 'in', 'which',
# 'we', 'are', 'still', 'making', 'discoveries']
stemmer = SnowballStemmer(language="english")
stemmed_words = list(map(lambda x: stemmer.stem(x), words))
print(stemmed_words)
# ['we', 'are', 'lucki', 'to', 'live', 'in', 'an', 'age', 'in', 'which',
# 'we', 'are', 'still', 'make', 'discoveri']
import collections
bag_of_words = collections.Counter(stemmed_words)
print(bag_of_words)
# {'we': 2, 'are': 2, 'in': 2, 'lucki': 1, 'to': 1, 'live': 1,
# 'an': 1, 'age': 1, 'which': 1, 'still': 1, 'make': 1, 'discoveri': 1}
实际上,如果我们想将文本转换为向量,不仅要考虑文本中的单词,还要考虑整个词汇表。假设我们的词汇表中还包括“i”、“you”和“study”,我们就可以从费曼的这句名言创建一个向量。
# bag of words vector
{'we': 2, 'are': 2, 'in': 2, 'lucki': 1, 'to': 1, 'live': 1,'an': 1, 'age': 1, 'which': 1, 'still': 1, 'make': 1, 'discoveri': 1, 'i': 0, 'you': 0, 'study': 0}
这种方法相当基础,它不考虑单词的语义意义,因此句子“the girl is studying data science”和“the young woman is learning AI and ML”在向量空间中不会接近彼此。
TF-IDF 模型
词袋模型的一个稍作改进的版本是TF-IDF(Term Frequency — Inverse Document Frequency,词频-逆文档频率)。它是两个度量值的乘积。
$$TF-IDF(t,d,D) = TF(t,d) \times IDF(t, D) $$
- 词频 (Term Frequency, TF) 表示单词在文档中出现的频率。最常见的计算方法是将该词在文档中的原始计数(类似于词袋模型)除以文档中的总词数。
$$TF(t,d)=\frac{number\ of\ times\ term\ t\ appears\ in\ the\ document\ d}{number\ of\ terms\ in\ document\ d}$$ - 逆文档频率 (Inverse Document Frequency, IDF) 表示单词提供的信息量。例如,像“a”或“that”这样的词不会给你关于文档主题的任何额外信息。相反,像“ChatGPT”或“生物信息学”这样的词可以帮助你确定领域(但不适用于这个句子)。它通过计算包含该词的文档数与总文档数的比例的对数来得到。IDF值越接近0,表示这个词越常见,提供的信息越少。
$$IDF(t,D)=log(\frac{total\ number\ of\ document\ in\ corpus\ document\ D}{number\ of\ documents\ containing\ term\ t})$$
最终,我们会得到一些向量,其中常见的词(如“I”或“you”)具有较低的权重,而多次出现在文档中的罕见词则具有较高的权重。这种策略会带来稍微更好的结果,但它仍然无法捕捉语义意义。
这种方法的另一个挑战是它会产生非常稀疏的向量。向量的长度等于语料库的大小。英语中大约有47万独特的单词(来源),因此我们将得到巨大的向量。由于一个句子通常不会超过50个不同的词,因此向量中99.99%的值将是0,不携带任何信息。鉴于这一点,科学家们开始思考密集向量表示。
词语潜在信息(Latent Information)与神经网络方法(Neural Network Method)
英文语境下,当我们谈论狗(dog)时,可能会使用除了“dog”之外的其他词语。我们是否应该在我们的分类方案中考虑像“canine”(犬类)或“feline”(猫科)这样的术语?我们需要为这些词添加一个新的项,例如 (dogx, caty, caninez, felinei)。
在英语中,一个大约30,000个词的词汇表对于这种词袋模型来说效果很好。在计算机世界中,我们可以比实体图书馆更平滑地扩展这些维度,但原则上问题类似。在高维度下,事情变得难以管理。随着组合爆炸,算法运行缓慢,稀疏性(大多数文档对大多数术语的计数为0)对统计和机器学习构成了问题。
因此,要将一本书投影到潜在空间(latent space)中,我们需要一个大矩阵,定义词汇表中每个观察到的术语对每个潜在术语的贡献程度。
有几个不同的算法可以从足够大的文档集合中推断出这一点:潜在语义分析(Latent Semantic Analysis, LSA),它使用术语-文档矩阵的奇异值分解(基本上是高级线性代数),以及潜在狄利克雷分配(Latent Dirichlet Allocation, LDA),它使用一种称为狄利克雷过程的统计方法。
我们使用词频作为某种更为模糊的主题性的代理。通过将这些词频投影到嵌入空间中,我们不仅可以降低维度,还可以推断出比原始词频更好地指示主题性的潜在变量。为此,我们需要一个定义良好的算法,如LSA,它可以处理文档语料库,找到从词袋输入到嵌入空间向量的良好映射。基于神经网络的方法使我们能够推广这一过程,并突破LSA的限制。
word2vec 模型
最著名的密集表示方法之一是word2vec,这是谷歌在2013年提出的,论文标题为“Efficient Estimation of Word Representations in Vector Space”,作者是Mikolov等人。
在这篇论文中提到了两种不同的word2vec方法:
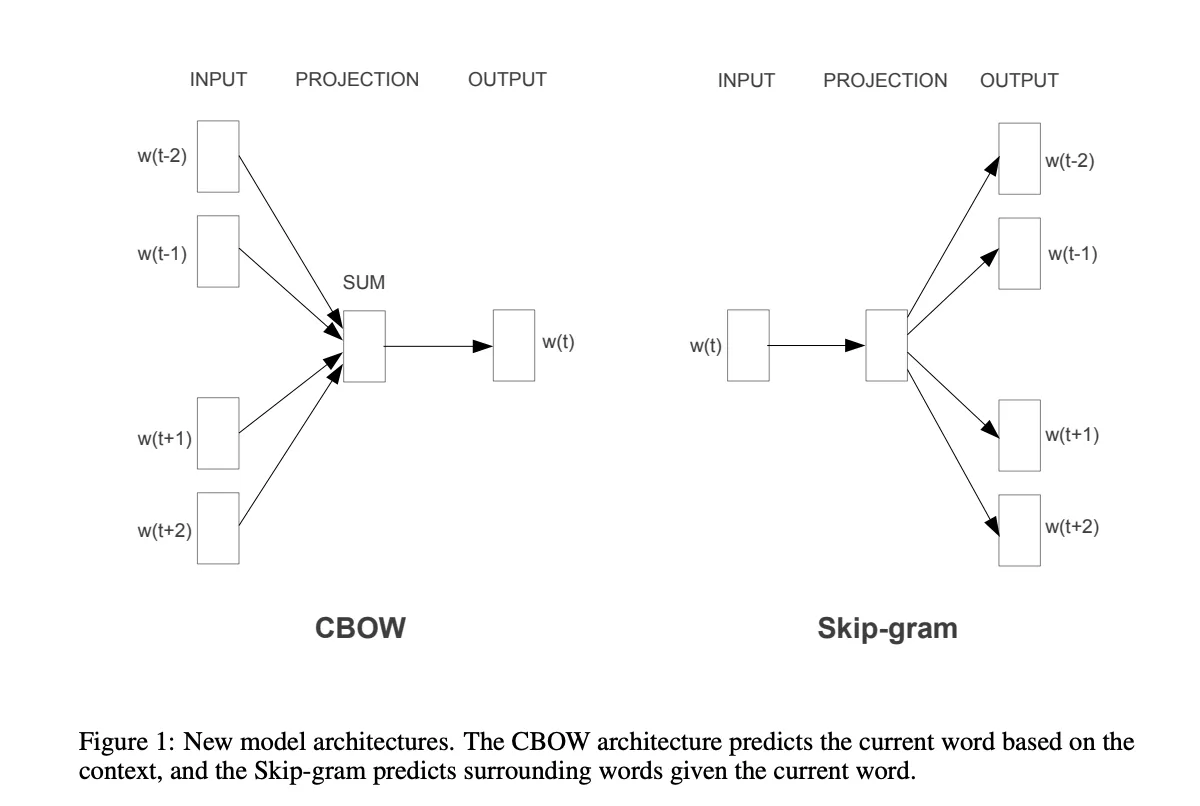
- Continuous Bag of Words (CBOW):在这种方法中,目标是根据上下文中的单词预测中间的单词。具体来说,给定一个单词序列,CBOW模型试图根据周围的单词预测中心单词。这种方法的优点是训练速度较快,因为每次更新都利用了更多的信息。
- Skip-gram:与CBOW相反,Skip-gram的目标是根据一个中心单词预测其周围的单词。也就是说,给定一个单词,模型试图预测这个单词周围的上下文单词。Skip-gram模型在捕捉罕见词的语义方面表现更好,但训练速度较慢,因为它每次更新只利用了一个单词的信息。
这两种方法都能生成词的密集向量表示,这些向量不仅包含了词的频率信息,还捕捉了词之间的语义关系。例如,使用word2vec生成的向量可以反映出“king”和“queen”之间的关系类似于“man”和“woman”之间的关系。
word2vec的成功在于它能够有效地将高维的词袋模型转化为低维的密集向量,同时保留了词的语义信息。这使得在自然语言处理任务中,如语义搜索、情感分析和机器翻译等,可以更高效地使用这些向量。
高维词向量的密集表示的核心思想是训练两个模型:编码器(encoder)和解码器(decoder)。以skip-gram模型为例,我们可以将单词“christmas”传递给编码器。编码器会生成一个向量,然后将这个向量传递给解码器,期望解码器能够输出“merry”、“to”和“you”等上下文单词。

具体步骤如下:
- 输入层:
- 在skip-gram模型中,输入是一个单词(例如“christmas”)。
- 编码器:
- 编码器将输入单词映射到一个固定长度的密集向量。这个向量通常被称为词嵌入(word embedding)。例如,如果词嵌入的维度是100,那么“christmas”会被映射到一个100维的向量。
- 解码器:
- 解码器接收这个100维的向量,并尝试预测该单词的上下文单词(例如“merry”、“to”、“you”)。解码器通常是一个多层神经网络,最后一层是一个softmax层,用于输出每个可能的上下文单词的概率分布。
- 损失函数:
- 模型的训练目标是最小化预测的上下文单词与实际上下文单词之间的差异。常用的损失函数是交叉熵损失(cross-entropy loss)。
训练过程:
- 前向传播:
- 输入单词“christmas”通过编码器生成一个100维的向量。
- 这个向量通过解码器,解码器输出一个概率分布,表示每个可能的上下文单词出现的概率。
- 反向传播:
- 计算预测的上下文单词与实际上下文单词之间的损失。
- 使用反向传播算法调整编码器和解码器的参数,以最小化损失。
通过这种方式,skip-gram模型能够生成高质量的词嵌入,这些嵌入不仅保留了词的频率信息,还捕捉了词之间的语义关系,为各种自然语言处理任务提供了强大的支持。这个模型开始考虑单词的意义,因为它是在单词的上下文中进行训练的。然而,它忽略了形态学(我们从单词部分可以获得的信息,例如,“-less”意味着缺乏某物)。这一缺点后来通过查看子词skip-grams在GloVe中得到了解决。
此外,word2vec只能处理单词,但我们希望对整个句子进行编码。因此,让我们进入下一个演进步骤,即transformers。
transformer 模型
下一次演变与 Vaswani 等人在论文“Attention is All You Need”中引入的变压器方法有关。变压器能够生成信息丰富的密集向量,并成为现代语言模型的主要技术。
变压器允许使用相同的“核心”模型,并针对不同的用例进行微调,而无需重新训练核心模型(这需要大量时间和成本)。这导致了预训练模型的兴起。其中一个早期流行的模型是Google AI的BERT(基于变压器的双向编码器表示)。
内部而言,BERT仍然像word2vec一样在词元级别上操作,但我们仍然希望获得句子嵌入。因此,一个简单的方法可能是取所有词元向量的平均值。不幸的是,这种方法的表现不佳。
这个问题在2019年随着Sentence-BERT的发布得到了解决。Sentence-BERT在语义文本相似性任务上超越了所有先前的方法,并允许计算句子嵌入。
text embeddings 计算验证
我使用阿里云大模型服务的text-embedding-v2来生成文本嵌入向量。结果,我们得到了一个1536维的浮点数向量。现在我们可以对所有数据重复这一过程,并开始分析这些值。
from dotenv import load_dotenv, find_dotenv
_ = load_dotenv(find_dotenv("./env/.env"))
import dashscope
from http import HTTPStatus
from pprint import pprint
resp = dashscope.TextEmbedding.call(
model=dashscope.TextEmbedding.Models.text_embedding_v2,
input="We are lucky to live in an age in which we are still making discoveries.",
dimension=1536,
)
pprint(resp['output']) if resp.status_code == HTTPStatus.OK else print(resp)
# output
# {'embeddings': [{'embedding': [0.022378576171554372,
# -0.027432455162420308,
# -0.00355793080956962,
# -0.030121118785560987,
# ...
# ],
# 'text_index': 0}]}
向量距离
嵌入实际上是向量。因此,如果我们想了解两个句子之间的相似程度,可以计算它们之间向量的距离。距离越小,表示它们的语义意义越接近。
可以使用不同的度量来测量两个向量之间的距离:
- 欧几里得距离(L2)
- 曼哈顿距离(L1)
- 点积
- 余弦距离
欧几里得距离(L2)
定义两点(或向量)之间距离的最标准方法是欧几里得距离或L2范数。这种度量在日常生活中最常用,例如,当我们谈论两个城镇之间的距离时。
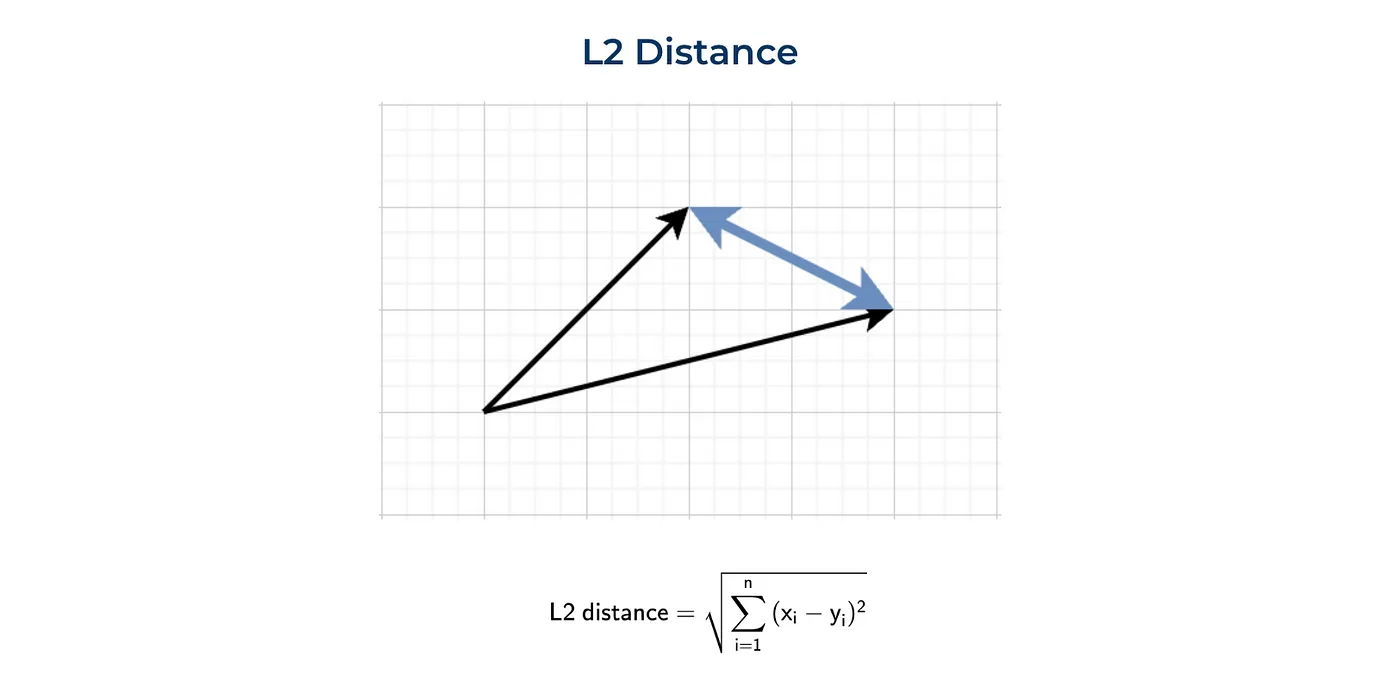
以下是L2距离的视觉表示和公式:
$$\text{L2距离} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + \cdots + (z_2 - z_1)^2}$$
曼哈顿距离(L1)
另一种常用的距离是L1范数或曼哈顿距离。这种距离是以纽约的曼哈顿岛命名的。该岛的街道布局呈网格状,两个点之间的最短路径将是L1距离,因为需要沿着网格行走。
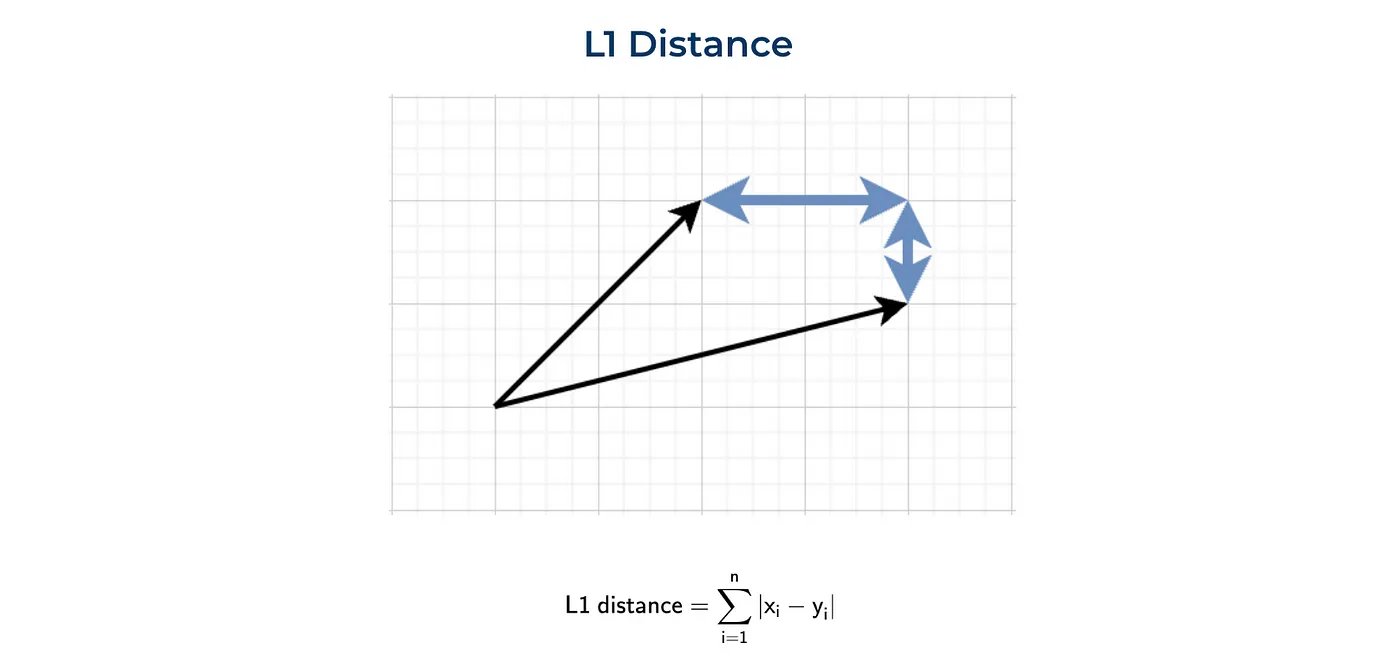
$$\text{L1距离} = \sum_{i=1}^{n} |x_i - y_i|$$
点积
另一种查看向量之间距离的方法是计算点积或标量积。以下是公式,我们可以轻松实现它:
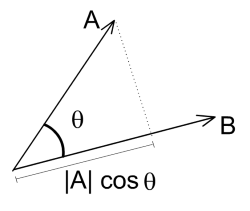
$$\text{点积} = \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta= \sum_{i=1}^{n} a_i b_i$$
这种度量的解释有点棘手。一方面,它显示了向量是否指向同一方向。另一方面,结果高度依赖于向量的大小。例如,让我们计算两对向量之间的点积:
- (1, 1) 和 (1, 1)
- (1, 1) 和 (10, 10)
在这两种情况下,向量都是共线的,但在第二种情况下,点积大十倍:2 对 20。
余弦相似度
余弦相似度经常被使用。余弦相似度是点积除以向量的模长(或范数)的归一化结果。
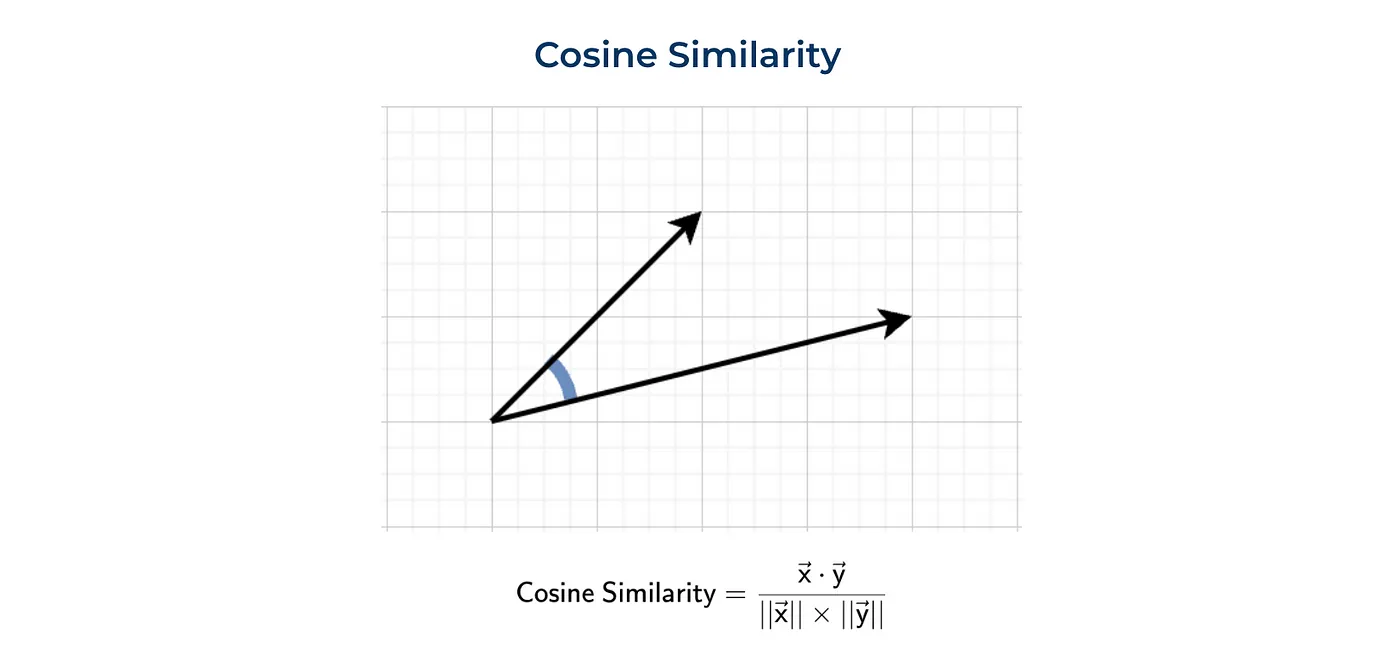
让我们谈谈这种度量的物理意义。余弦相似度等于两个向量之间的夹角的余弦值。向量越接近,度量值越高。
$$\text{余弦相似度} = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$$
距离计算方法选择
你可以使用任何距离来比较你得到的嵌入。例如,我计算了不同聚类之间的平均距离。无论是L2距离还是余弦相似度,都展示了类似的结果:
- 同一聚类内的对象比与其他聚类的对象更接近。解释我们的结果时需要注意,对于L2距离,更接近意味着距离更低;而对于余弦相似度,更接近的对象的度量值更高。不要混淆。
- 我们可以发现某些主题彼此非常接近,例如,“政治”和“经济”或“人工智能”和“数据科学”。
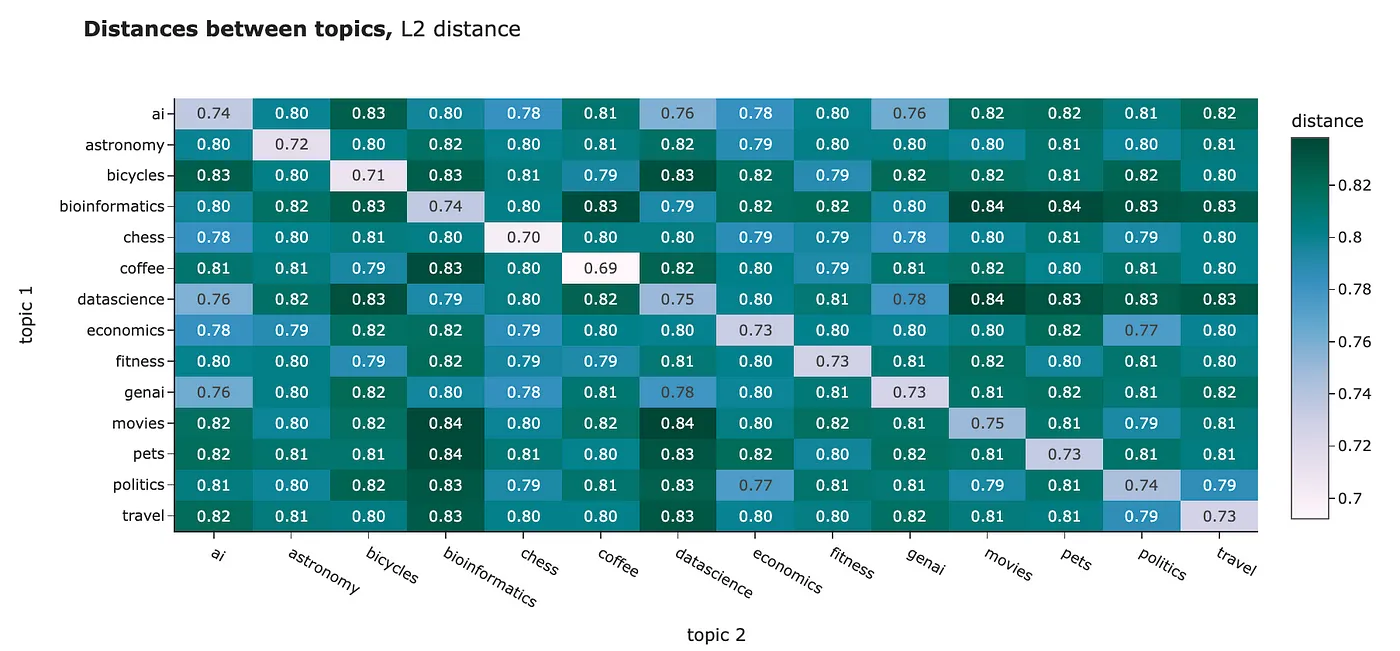
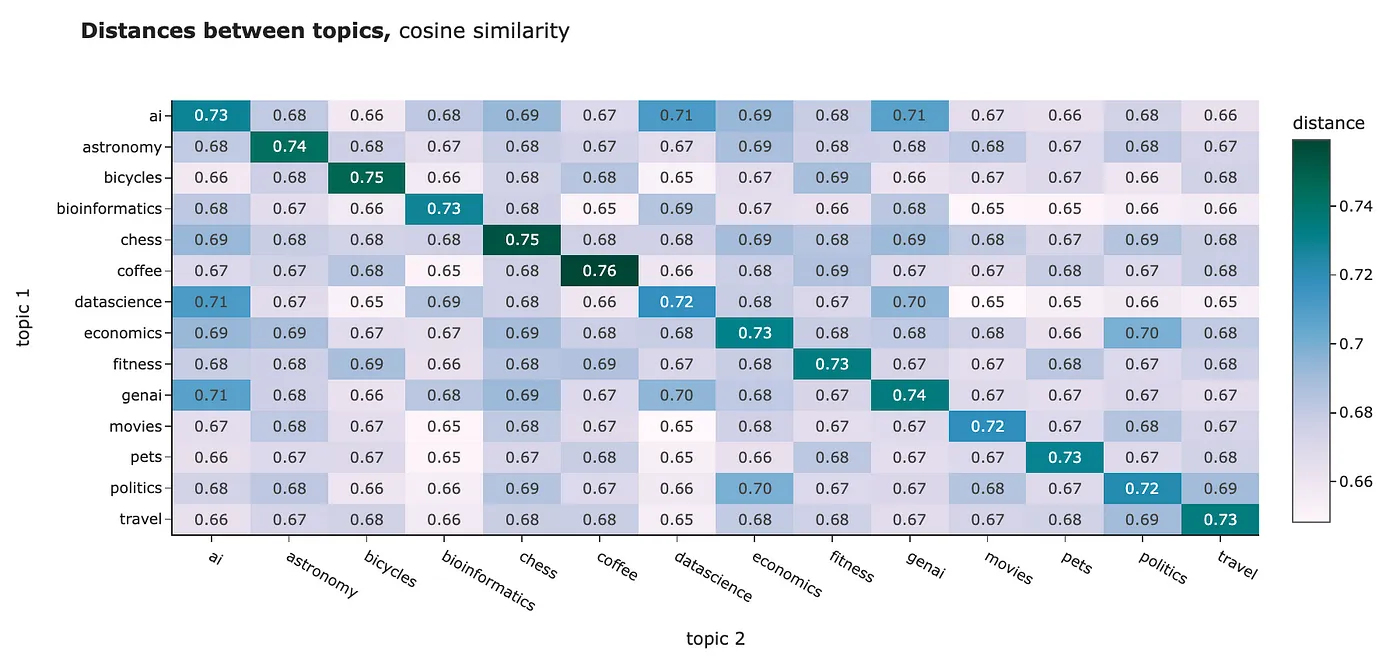
然而,对于NLP任务,最佳实践通常是使用余弦相似度。背后的原因包括:
- 余弦相似度的范围在-1到1之间,而L1和L2距离是没有界的,因此更容易解释。
- 从实际角度来看,计算点积比计算欧几里得距离的平方根更有效。
- 余弦相似度受维度诅咒的影响较小(维度越高,向量之间的距离分布越窄)。
向量可视化
理解数据的最佳方式是将其可视化。不幸的是,嵌入有1536个维度,因此直接查看数据非常困难。然而,有一种方法:我们可以使用降维技术将向量投影到二维空间中。
注意: 以下可视化数据来自 Stack Exchange Data Dump,由于数据量是92.3G,我就没有自己本地跑可视化结果,本文可视化视图来自 Mariya Mansurova 的Text Embeddings: Comprehensive Guide。
PCA
最基本的降维技术是主成分分析(PCA)。
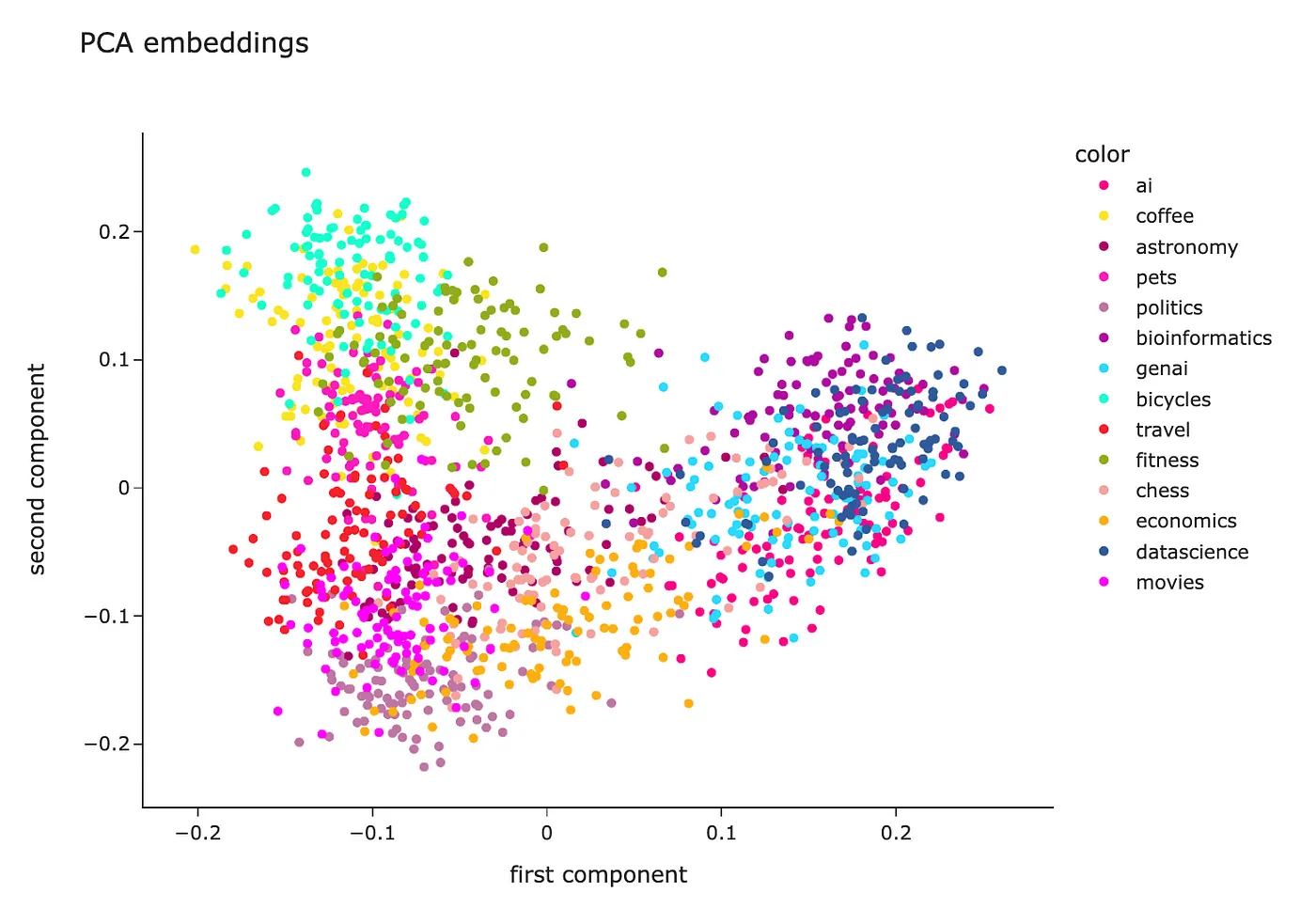
t-SNE
PCA是一种线性算法,而在现实生活中大多数关系是非线性的。因此,由于非线性问题,我们可能无法很好地分离聚类。让我们尝试使用一种非线性算法——t-SNE,看看它是否能显示出更好的结果。
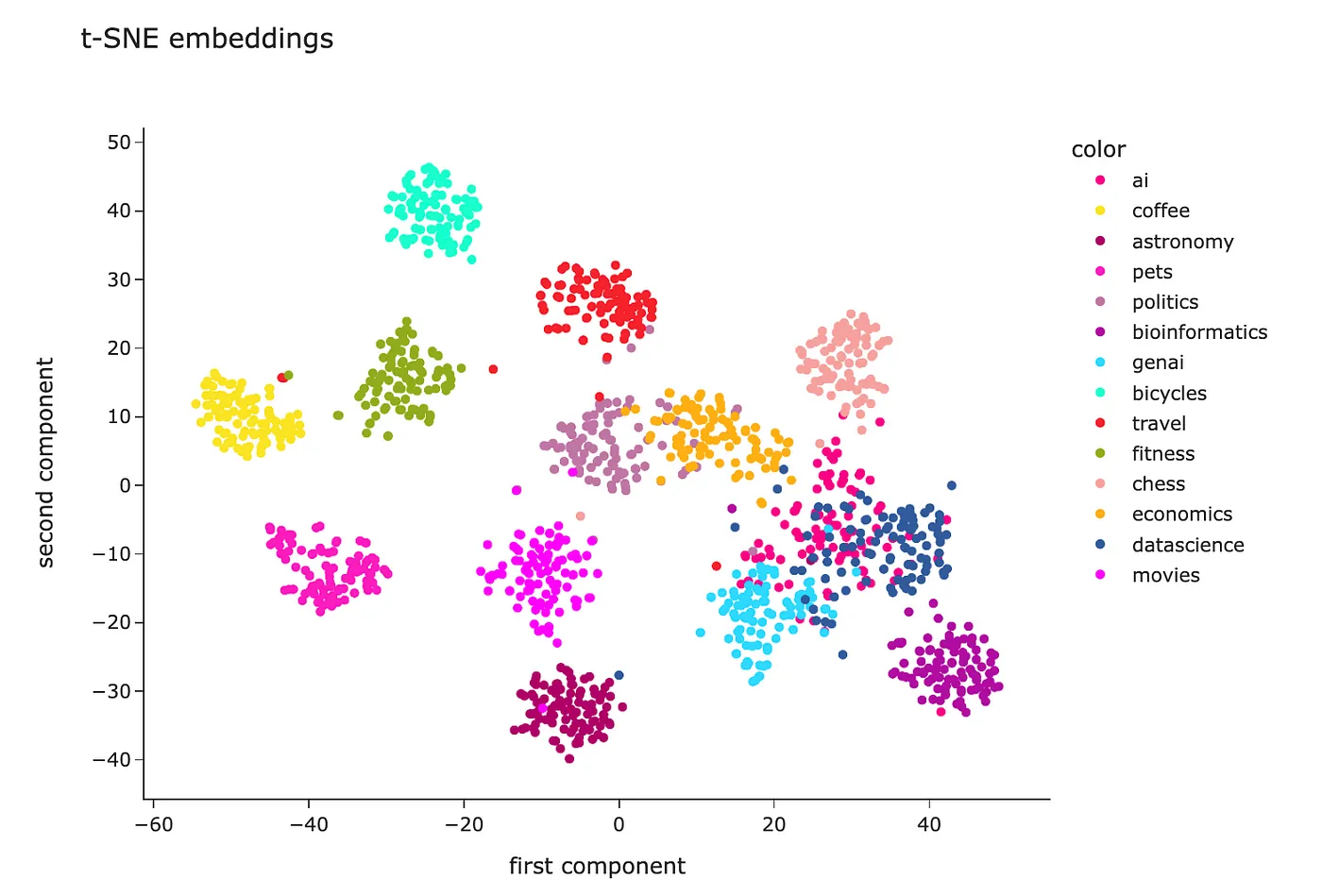
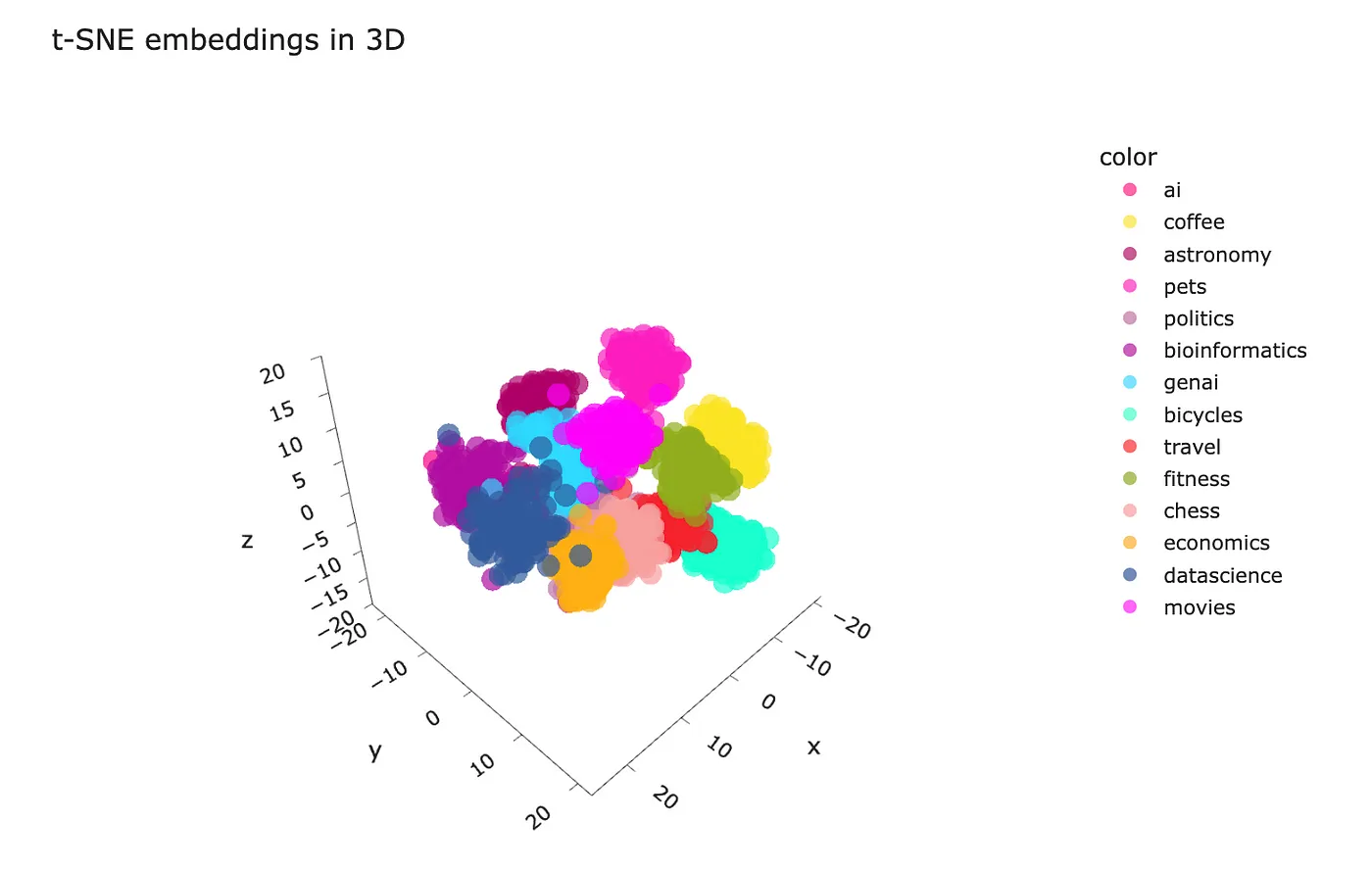
根据t-SNE可视化的推理
来源内容:
Is it safe to drink the water from the fountains found all over
the older parts of Rome?
When I visited Rome and walked around the older sections, I saw many
different types of fountains that were constantly running with water.
Some went into the ground, some collected in basins, etc.
Is the water coming out of these fountains potable? Safe for visitors
to drink from? Any etiquette regarding their use that a visitor
should know about?
t-SNE嵌入:
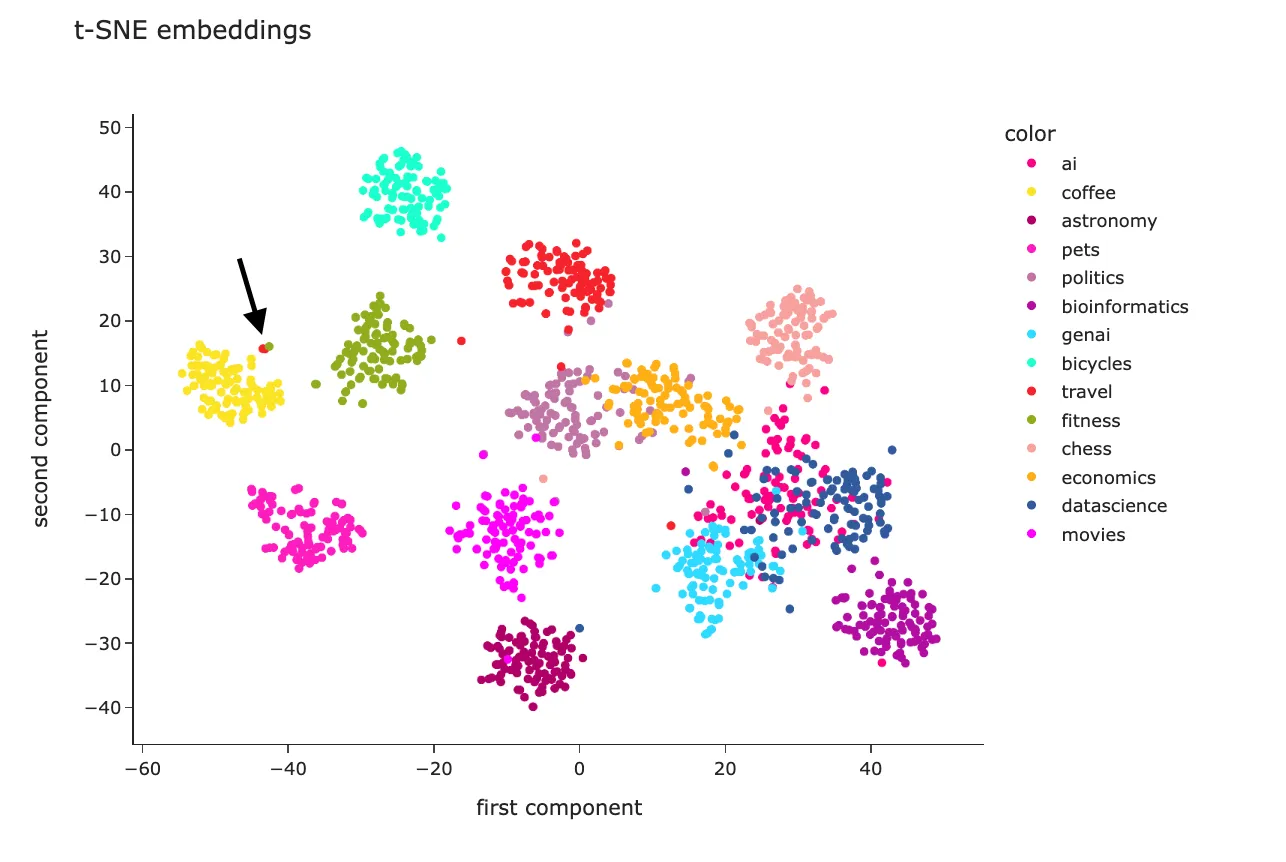
我们可以在t-SNE可视化中找到这条内容,并发现它实际上靠近咖啡聚类。
这句话的意思是,在t-SNE可视化中,这条关于罗马喷泉水的问题被映射到了一个与咖啡相关的话题附近。这可能表明,尽管这两者看似不相关,但它们在某些方面存在一定的语义相似性,或者在数据集中它们经常一起出现。


Public discussion